常见的排序算法（一）

发表于 | 分类于

前言

好久没写博客了，今天就来写一篇跟排序算法有关的博客
说到排序算法，首先想到的有快排，堆排序等优秀的算法，你知道排序算法有哪些分类吗？

一、内排序、外排序

内排序：指数据直接在内存中进行，无需借助外存
外排序：由于数据量太大，内存不能一次性装完，需要借助外存储器才能完成
其实对于外排序，处理的时候大多数也会使用到内排序，也就是将一部分数据从磁盘加载进来然后使用内排序完后再写回磁盘
但也有直接外排序的算法，比如：多路平衡归并排序，置换——选择排序，最优归并树（PS：这些都没了解过hhhh）
但是常见的内排序算法就有很多了：冒泡、选择、插入、希尔、归并、快速、堆排序、计数排序、桶排序这些都是常见的排序算法

二、稳定性

何为稳定性？
比如这样：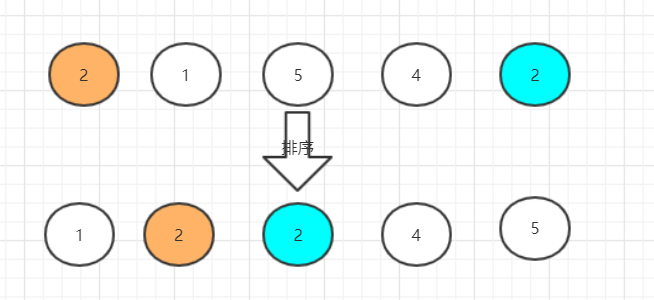
排序1
还没排序前，橙色的2在蓝色的2前面
排完序后橙色的2还是在蓝色的2前面
如果能做到这种特性，那么就认为该排序算法是稳定的

为什么需要稳定的排序算法呢？
因为有时候我们不止依赖一个特性来排序，比如订单有金额跟下单时间的特性，我们按金额大小排序，如果金额相等，就要求按下单时间来排序。如果要求你来做，你怎么实现呢？
如果有稳定的排序算法，我们可以先按下单时间来排序，拍完后就再按照金额来排序，这样就能符合我们如果金额相等就按下单时间来排序
因为先按时间排好序后，再用稳定的排序算法按金额排列，不会出现相等金额的时间乱序的情况

稳定性的排序算法有：冒泡排序、插入排序、归并排序、希尔排序
不稳定的排序算法有：选择排序、快速排序

三、是否需要辅助空间

不需要申请额外内存的排序，也叫做原地排序，常见的原地排序算法有：冒泡、选择、插入、希尔、快速、堆排序
而向归并、桶排序、计数排序，它们虽然时间复杂度很快，但需要借助额外的内存空间
所以选择合适的排序算法的时候，也需要考虑是否需要额外的内存空间，比如你的内存只有2G，但你有1.5G的数据需要排序，你得考虑申请额外空间是否够用

四、平均时间复杂度

O(n^2)：冒泡排序、选择排序、插入排序
O(nlog2n)：希尔排序
O(nlogn)：归并排序、快速排序、堆排序
O(n)：计数排序、桶排序
也许有人会问，竟然计数跟桶排序能做到O(n)的时间复杂度，为什么他们不会经常出现在我们的视野呢？而是快排或者堆排序出现的比较多？
你学下去不就知道了
下面分析的时间复杂度都是平均时间复杂度

冒泡排序

冒泡的思想为：每次比较相邻的元素。如果第一个比第二个大，交换他们，然后按照这个思想往后遍历
每次遍历完，最后的元素都是最大的

看一下经过一次冒泡排序后，数据经过了哪些改变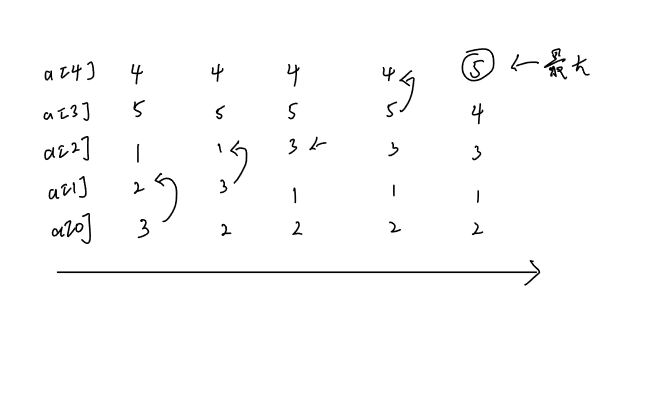
冒泡1
可以看到，无序的数据经过一次冒泡后，5作为最大的数据被排在了末尾
再看一下完整的过程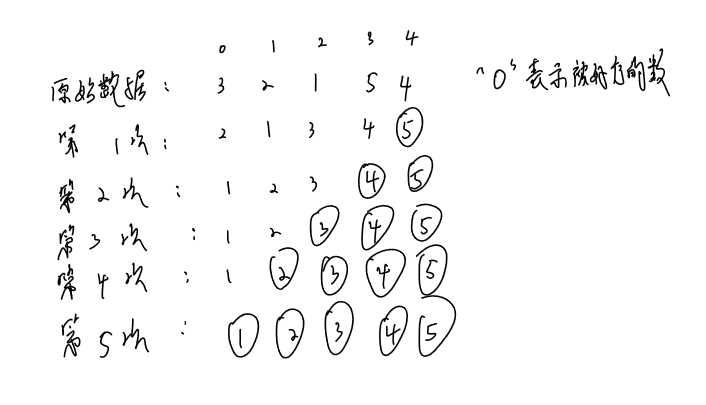

可以看到冒泡的每一次操作都能从中将最大的数移动到末尾，这样最后的数据就是有序的了

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
package sort_alorgithm;

import java.util.Arrays;

/**
 * 冒泡排序
 *      稳定性：稳定
 * 时间复杂度分析：
 *      最好情况：O(n)
 *      最坏：O(n^2)
 *      平均：O(n^2)
 * 空间复杂度：O(1)没有借助其他空间
 * 稳定性：稳定
 *
 * @author SouthLight-Lin on 2019/6/7
 */
public class BubbleSort{
    /**
     * 算法步骤：
     *      比较相邻的元素。如果第一个比第二大，就交换他们两个
     *      对每一对相邻元素做同样的工作，每次做完，最后的元素会是最大的数
     *      重复以上步骤 ，除了最后一个
     */

    public static int[] sort(int[] source){
        // 对source进行拷贝，不改变参数的内容
        int[] arr = Arrays.copyOf(source, source.length);

        for (int i = 1; i < arr.length; i++) {
            // 设定标记，若为true，
            // 表示本次循环没有进行交换，数组已经有有序
            boolean flag = true;
            for (int j = 0;j<arr.length-i;j++){
                if (arr[j]>arr[j+1]){
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                    flag = false;
                }
            }
            if (flag){
                break;
            }
        }
        return arr;
    }

    public static void main(String[] args) {
        int[] source = {2,5,4,3,8};
        int[] result = sort(source);
        for (int i = 0; i < result.length; i++) {
            System.out.print(result[i] + " ");
        }
    }
}

上述代码中，加入了一个boolean类型的flag，为了减少循环的次数，如果遍历的过程中发现没有数据交换，那么就可以认定为该组数据已经有序，后面的操作都不用做了，直接跳出

时间复杂度：O(n^2）
空间复杂度：O(1)
稳定性：稳定排序

选择排序

思想：每次遍历数据，从中选出最大的数（最小也可以），换到数据末尾
选择排序
代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

package sort_alorgithm;

import java.util.Arrays;

/**
 * 选择排序
 * @author SouthLight-Lin on 2019/6/8
 *
 * 时间复杂度：
 *      最好：O(n^2)
 *      最坏：O(n^2)
 *      平均：O(n^2)
 * 空间复杂度：O(1)
 * 稳定性：不稳定
 */
public class SelectionSort {

    /**
     * 算法步骤：
     *      首先在未排序序列中找到最小（大）的元素，存放到排序序列的起始位置
     *      再从剩余未排序的元素中找到最小（大）元素，然后放到已排序序列的末尾
     *      重复第二步，直到所有元素排列完毕
     */

    public static int[] selectionSort(int[] source){
        int[] arr = Arrays.copyOf(source, source.length);
        // 总共需要N-1此比较
        for (int i = 0; i < source.length-1; i++) {
            int min = i;
            // 每轮需要N-i此比较
            for (int j = i+1; j < source.length; j++) {
                if (arr[j] < arr[min]) {
                    // 记录目前能找到的最小值元素的小标
                    min = j;
                }
            }

            // 将找到的最小值与i位置的数交换
            if (i != min){
                int tmp = arr[i];
                arr[i] = arr[min];
                arr[min] = tmp;
            }
        }
        return arr;
    }

    public static void main(String[] args) {
        int[] source = {4,2,3,6,5};
        int[] result = selectionSort(source);
        for (int i = 0; i < result.length; i++) {
            System.out.print(result[i] + " ");
        }
    }
}

时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：非稳定排序

插入排序

你应该玩过扑克牌，当你开始整理你的牌的时候，那你可能习惯一张一张的抽出牌并把它插入到正确的位置，插入排序的思想正是如此
从前往后遍历数据，以第一个数据为基准有序数据，将数据插入到正确的位置
其实实现的时候，插入是指将前面的数据比目前该数据大的往后移动，腾出空间插入
插入排序
代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package sort_alorgithm;

import java.util.Arrays;

/**
 * 插入排序
 * 时间复杂度：
 *      最好：O(n)
 *      最坏：O(n^2)
 *      平均：O(n^2)
 * 空间复杂度：O(1)
 * 稳定性：稳定
 *
 * @author SouthLight-Lin on 2019/6/8
 */
public class InsertSort {
    /**
     * 算法步骤：
     *      将待排序列第一个元素看成是一个有序序列，把第二个元素到最后一个元素当成是未排序序列
     *      从头到尾一次扫描未排序序列，将扫描到的每个元素插入到有序序列的适当位置。（如果待插入的元素与有序
     *      序列中的某个元素相等，则将待插入元素插入到相等元素的后面）
     *
     * 抽象：这个算法跟我们平时打扑克时，整理扑克的思路是一样的
     */

    public static int[] insertSort(int[] source){
        int[] arr = Arrays.copyOf(source, source.length);

        // 从下表为1开始，因为下标为0的值默认是有序的
        for (int i = 1; i < arr.length; i++) {
            int tmp = arr[i];

            int j = i;
            // 从末尾开始比较，如果比j-1位置的数小
            // 则前一个数后移
            while (j > 0 && tmp < arr[j-1]){
                arr[j] = arr[j-1];
                j--;
            }

            // 存在比其小的数，插入
            if (i!=j){
                arr[j] = tmp;
            }
        }

        return arr;
    }

    public static void main(String[] args) {
        int[] source = {4,2,3,6,5};
        int[] result = insertSort(source);
        for (int i = 0; i < result.length; i++) {
            System.out.print(result[i] + " ");
        }
    }
}

时间复杂度：O(n^2)
空间复杂度：O(1）
稳定性：稳定排序

希尔排序

希尔排序是对插入排序的改进，有实验证明，如果数据时部分有序的数据，使用插入排序效率会很高，所以希尔排序就是在这点上改进来的
针对插入排序的两点性质而提出的改进方法：
1、 插入排序在对几乎已经排好序的数据操作时，效率高，可以达到线性排序的效率 2、 但插入排序一般来说效率是低效的，因为每次插入排序每次只能将数据移动一位

希尔排序的基本思想：
将待排序的记录分割成为若干个子序列，分别进行插入排序，待整个序列记录“基本有序时”，再对整体进行插入排序

希尔排序
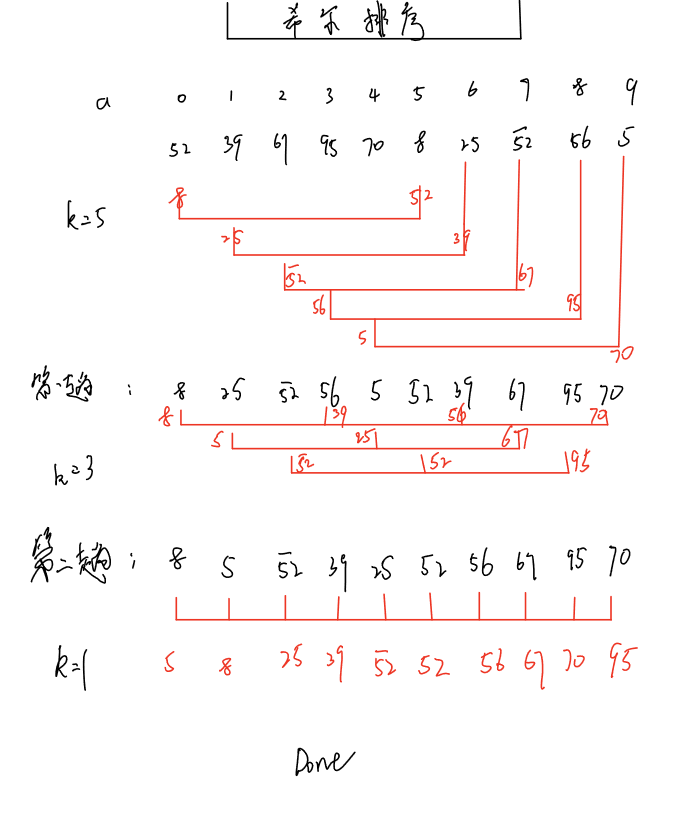
代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
package sort_alorgithm;

import java.util.Arrays;

/**
 * 希尔排序：
 *      又称为增量排序，是插入排序的一种更加高效的改进版本。但是希尔排序是不稳定排序
 * 希尔排序是针对插入排序的一下两点性质而提出改进方法：
 *      1、插入排序在对几乎已经排好序的数据操作时，效率高，可以达到线性排序的效率
 *      2、但插入排序一般来说效率是低效的，因为每次插入排序每次只能将数据移动一位
 * 基本思想：
 *      希尔排序的思想是将整个待排序的记录分割成为若干个子序列分别进行直接插入排序，待整个序列中的
 *      记录“基本有序”时，再对全体记录进行依次直接插入排序
 *
 * 时间复杂度：
 *      最好：O(nlog^2n)
 *      最坏：O(nlog^2n)
 *      平均：O(nlogn)
 * 空间复杂度：O(1)
 * @author SouthLight-Lin on 2019/6/9
 */
public class ShellSort {
    /**
     * 算法实现：
     *      1、选择一个增量序列t1,t2,...,tk（tk=1）；
     *      2、按增量序列个数k，对序列进行k趟排序;
     *      3、每趟排序，根据对应的增量ti，将待拍序列分割成若干长度为m的子序列，
     *      分别对各子序列进行直接插入排序。
     *      仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度
     */
    public static int[] shellSort(int[] source){
        int[] arr = Arrays.copyOf(source, source.length);

        // 设置增量因子
        int gap = 1;
        while(gap < arr.length){
            gap = gap * 3 +1;
        }

        while (gap > 0){
            for (int i = gap; i < arr.length; i++) {
                int tmp = arr[i];
                int j = i-gap;
                while (j>=0 && arr[j] > tmp){
                    arr[j+gap] = arr[j];
                    j -= gap;
                }
                arr[j+gap] = tmp;
            }
            gap = (int) Math.floor(gap/3);
        }
        return arr;
    }

    public static void main(String[] args) {
        int[] source = {8,3,9,5,1,4,7,6,2,0};
        int[] result = shellSort(source);
        for (int i = 0; i < result.length; i++) {
            System.out.print(result[i] + " ");
        }
    }

}

时间复杂度：O(nlog2n)
空间复杂度：O(1)
稳定性：非稳定排序

总结

今天聊了冒泡、选择、插入、希尔排序四种算法，其实这四种算法各有好坏，比如前三种实现起来简单，但平均时间复杂度高一些，选择排序无论情况怎么样时间复杂度都是O(n^2)，希尔排序算是今天这四种算法里面最快了