今天趁着周末,来聊聊两道题目。周末做了两家公司的秋招笔试——小米、网易娱乐,虽然笔试类型不同,但最后都有编程题。而且编程题中刚好都考了二叉树的算法题,而且不是正规的二叉树题目,算是二叉树的变种题,惭愧的是小米的那道二叉树想到了解决方案,无奈最后时间有限,只搭了个框架,没有做出来
PS:笔试虐我千百遍,我待笔试如初恋
题目一:中根遍历二叉树
题目是这样的:输入一个字符串,该字符串是二叉树先根遍历比如输入1(2,3),输出该二叉树的中根遍历序列
输入的先根遍历序列,比如1(2,3),它对应节点的结构为: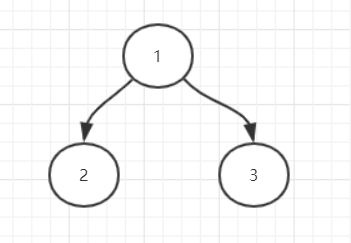
也就是括号里面代表子节点,括号外面是父节点
再来举个例子,例如输入:1(2(4,),3(,5)),对应的树结构为: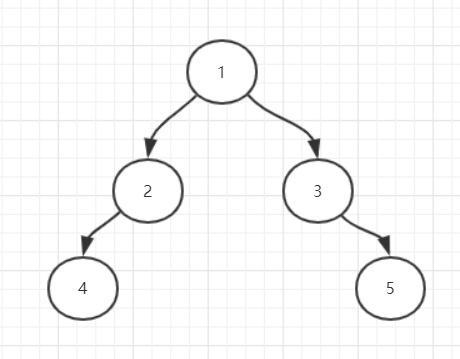
如果输入:1 ,那么对应的只有1这个节点,没有子节点
方案
刚开始看到括号,脑子里立马想到的是使用栈,但比划了许久后发现使用栈行不通,所以改变了一下策略
这道题的关键,只要能通过输入的字符串构造二叉树就好办了。先来看下1(2,3)这个字符串怎么构造节点,其实很简单嘛,括号外面就是父节点,逗号左边就是左子节点,右边就是右子节点
单个括号很容易解决,那多个括号镶嵌怎么解决?我们就一个一个解决,用分治思想,因为我们解决单个括号后,还要回退回去,跟父节点匹配,所以 分治法 就是这道题的关键
对于输入:1(2(3,4(,5)),6(7,)) 我画个图分析下: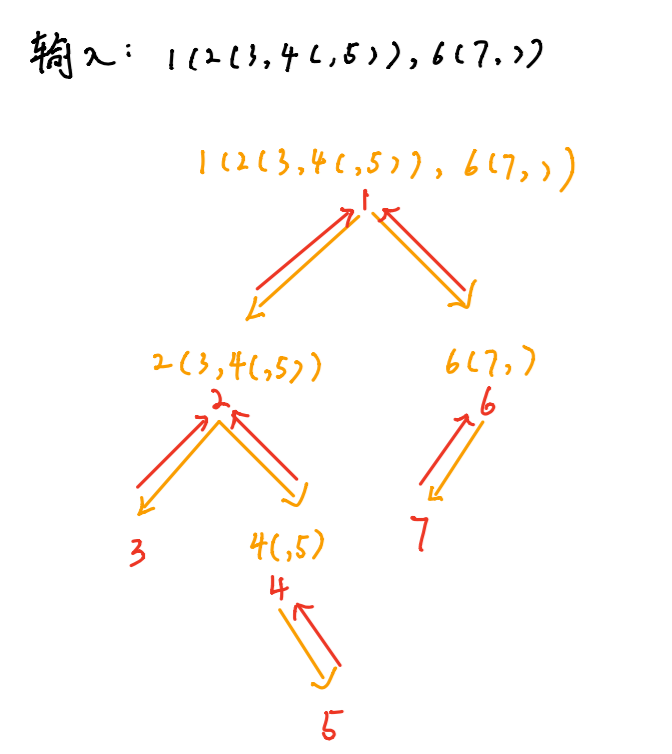
构建出来的二叉树为: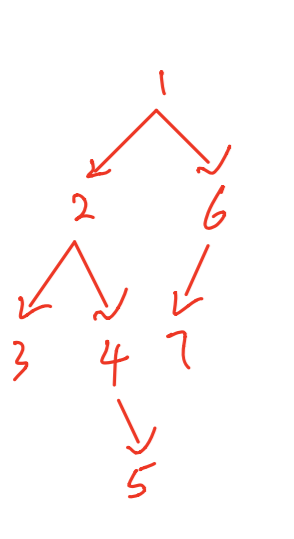
整个解题过程大概就是这样,但还有一个关键问题没解决:怎么截取字符串?也就是怎么从1(2(3,4(,5)),6(7,))截取出2(3,4(,5))和6(7,)
我们可以写个函数,该函数可以找到括号中分割的逗号下标,这样就可以把字符串划分为左右子串两部分,代表两个节点
我的思路是这样的:
1、先判断该字符串是否有左节点
2、如果没有左节点,例如1(,3(4,5)),那么返回的下标就为2
3、如果有左节点,还要在分下情况
3.1、如果左节点没有子节点,返回3,例如1(2,3(4,5))
3.2、如果左节点有子节点,那么就循环一直找。例如1(2(3,4(,5)),6(7,)) 从’3’开始,定义一个sum=1(代表有一个左括号还没匹配),每遇到一个左括号sum++,遇到右括号sum–,直到sum==0终止条件,返回当前下标加一,idx+1
1 | /** 找到分割的逗号下标 **/ |
画个图就知道了:

可能有人会担心越界问题,但我们只要严格控制调用这个函数时,字符串长度一定到大于6即可
好了,只要分割到字符串的个数小于等于6,就能使用开头我们讲的单个括号生成节点的方案,然后递归回溯回去就能构成一棵二叉树
但题目要求是求中根遍历,二叉树我们构建出来了,那么中根遍历就很容易了
1 | static StringBuilder builder = new StringBuilder(); |
我们声明一个全局变量,记录遍历的节点值,使用递归的方法就可完成该题目
完整代码:
1 | package bishi.xiaomi; |
题目二:递增树
这道题是网易娱乐的笔试题,题目是这样的,输入整数n,代表n个节点,然后接下来的n行,每行代表第k个节点(k从0开始),每行输入3个数,第一个数代表节点的值,第二个值代表左子节点的序号,第三个值代表右子节点的序号,如果没有子节点就输入-1,这样输入的就是一棵二叉树。判断这颗二叉树是不是递增树,递增树:树的每一层值的和比下一层值的和小
是不是看到题目描述看不懂,没关系,我也就看了十几分钟才看得懂他到底想说什么。
比如输入:n=3,接下来输入3行
1 1 2
2 -1 -1
3 -1 -1
一行代表一个节点,第一个数代表该节点的值,第二个数为左子树的序号,也就是1代表下面一行的值为2的节点,第三个数代表右子树的序号,也就是2代表白值为3的节点,画图如下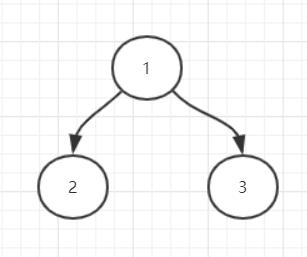
关键是理解每行输入的后面两个数,对应输入的行数的第n+1行
方案
要判断这棵树是不是递增树,我们也要首先把输入的节点构造成一个二叉树
我们先声明树节点的Class类
1 | static class TreeNode{ |
前三个属性很好理解,后面三个是为了后续操作加上的。
因为我想先用TreeNode[] 数组存放输入的各个节点,所以leftIdx和rightIdx分别对应在数组中的下标。
然后遍历一遍数组,让数组中的各个节点左右指针连接起来
如图: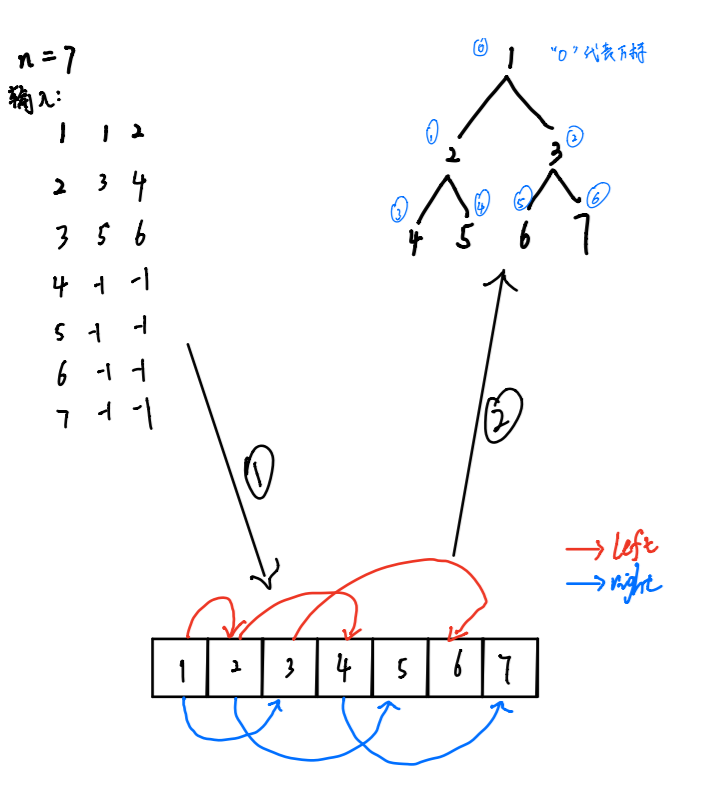
经过步骤1后形成了数组TreeNode[],已经可以构成一棵二叉树了,但是我们不知道哪个是根节点,所以TreeNode的属性maxDepth派上用场了。
我们写个函数maxDepth(TreeNode node),计算数组中每个节点的最大深度,然后从数组中找出最大的maxDepth,该节点就是根节点了
求每个节点的最深度这个函数也不难写
1 | /** 求每个节点的深度 **/ |
只要得到根节点,二叉树就算构建完成了,回到题目,判断树是否为递增树,我的思路是:我们维护一个maxDepth大小的int[]数组res,每个值代表该层的总和值。我们如果能将这个res计算处理,遍历一遍就知道是不是递增树了
这个函数也不难写,我们可以通过深度搜索DFS,函数接受三个值——节点,res数组,当前层数i。dfs(TreeNode root,int[] res, int i), 递归搜索知道叶节点即可
1 | /** 深度搜索,计算每一层的和 **/ |
完整代码如下:
1 | package bishi.wangyiyouxi; |
总结
这两道算法题都是很有代表性的,一方面考察我们构造二叉树的能力,第二方面考察我们对递归和分治法运用。说实话大厂的笔试是真的难,前几次笔试的题没有一道能跑通过,笔试完就挂了,连面试的机会都没有,我不服气,我就不信没一道能跑通过!终于,昨晚的笔试,四道算法题终于跑过了三道,算是一种鼓励吧。算法这种东西,还是得多学多练才能掌握~~~